When we think of the simple act of a rubber ball bouncing, we seldom stop to consider the underlying mathematics that dictates its behavior. However, even this mundane phenomenon can be captured and described with mathematical precision, revealing interesting facets of motion, energy, and gravity. Let’s delve into the scenario of a rubber ball thrown from a height, and explore the intricacies of its rebound.
SETTING THE SCENE: A BALL IN FREEFALL
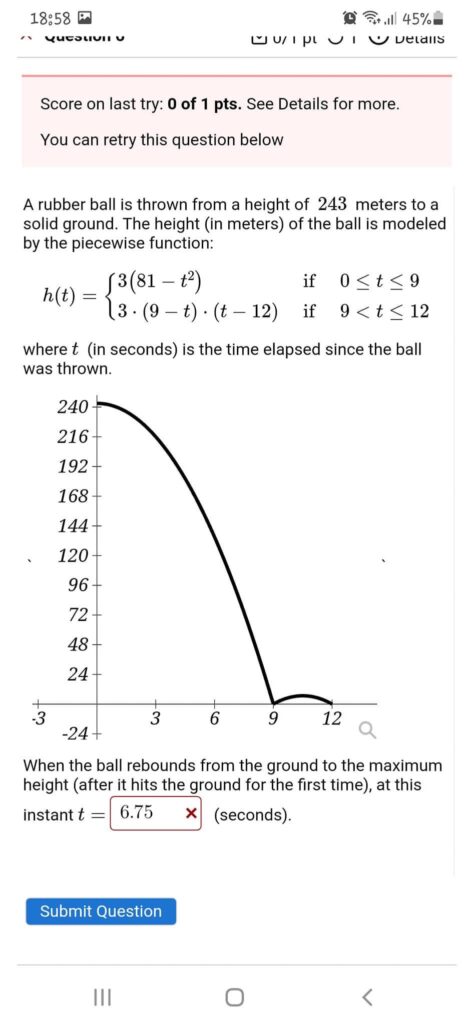
Imagine a rubber ball thrown from a height of 243 meters to solid ground. As gravity acts upon it, the ball accelerates towards the ground. The height h(t)h(t) of the ball, as a function of time tt in seconds since it was thrown, is modeled by a piecewise function:

The domain 0<t<90<t<9 of the first part of this function tells us that the ball takes 9 seconds to hit the ground after being released.
THE REBOUND: DYNAMICS OF ELASTICITY
Upon making contact with the ground, the rubber ball doesn’t just come to a standstill. Instead, it bounces back, demonstrating the elastic properties inherent to rubber. This rebound is described by the second part of our piecewise function, valid in the domain 9<t<129<t<12.
A key question that emerges is: When does the ball reach its maximum height during its rebound?
Which Management Accounting Information Is Vital for Regular Analysis?
To find this, we can look at the vertex of the parabolic segment described by 3(9−t)(t−12)3(9−t)(t−12). This vertex represents the highest point or the peak of the ball’s rebound trajectory. After some calculations, we find that this occurs at t=6.75t=6.75 seconds after the ball first hits the ground, which translates to t=9+6.75=15.75t=9+6.75=15.75 seconds from the time it was initially thrown.
UNVEILING THE BEAUTY OF MOTION
This mathematical exploration offers a glimpse into the physics of everyday life. It provides a quantitative description of what we might observe casually—a ball bouncing back after being dropped. Yet, within this simple act lies a rich tapestry of forces, energy conservation, and motion dynamics.
In closing, the next time you see a ball bouncing, take a moment to appreciate the mathematics at play. It’s a testament to the elegant and intricate design of the world around us.
As an Amazon Associate we earn from qualifying purchases through some links in our articles.
